对于大型语言模型而言,生成更长、更复杂的推理链,往往意味着巨大的计算成本。为了解决这一难题,田渊栋团队在 2024 年提出的「连续思维链」 (Coconut) 提供了一种全新的范式,它将推理轨迹保留在连续的隐空间中,而非离散的文字符号。现在配资平台股票配资,他们与 Stuart Russell 团队的最新合作研究则从理论上回答了一个核心问题:这种高效的推理范式是如何在训练中自发产生的?答案指向了一种关键机制——叠加的涌现 。
大型语言模型(LLM)在许多复杂任务上展现出了强大的推理能力,尤其是在引入思维链(CoT)之后。然而,长思维链在复杂任务中的推理成本极高,因此,近期有不少研究在尝试寻找更高效的测试时扩展方法,以期望更高效地提升模型的推理能力。
一种前景较为可观的方法是田渊栋团队在 2024 年提出的「连续思维链」(Chain-of-Continuous-Thought,简称 Coconut)。与传统的 CoT 不同,连续思维链是将模型的推理轨迹保存在连续隐空间中,而非回投到离散的 token 空间。这种做法不仅在理论上具有多项优势,在实验中也带来了显著性能提升。参阅我们之前的报道《田渊栋团队论文火了!连续思维链优于 CoT,打开 LLM 推理新范式》。
然而,若要让连续思维链更高效、更稳定地扩展到更复杂的推理任务,就必须更深入地理解它的内部机制。
该团队 2025 年的研究《Reasoning by superposition: A theoretical perspective on chain of continuous thought》已从理论上指出,连续思维链的一个关键优势在于它能使模型在叠加(superposition)状态下进行推理:当模型面对多个可能的推理路径而无法确定哪一个是正确时,它可以在连续空间中并行地保留所有可能的路径,而不像离散 token 那样必须选择单一路径。
具体来说,该研究将一类推理任务抽象为有向图可达性(a directed graph reachability)问题 —— 即判断从给定起点节点能否到达目标节点。
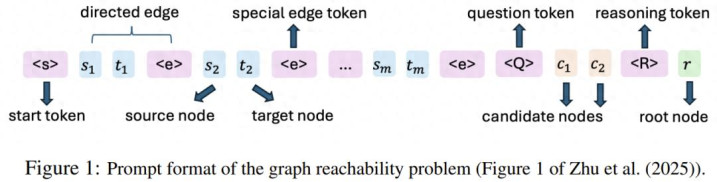
他们进一步证明,只需一个两层 Transformer,经过 O (n) 次连续思维解码(其中 n 为图中节点数量),即可通过特定参数构造有效地解决该问题。
因此,一个自然的问题随之而来:梯度下降训练能否自然地收敛出这种结构?我们能否在理论上证明这一点?
近日,田渊栋与 Stuart Russell 两个团队合力,发表了论文《叠加的涌现》,对这个问题给出正面回答。本论文一作 Hanlin Zhu(竺涵林)为加利福尼亚大学伯克利分校(UC Berkeley)电子工程与计算机科学系博士生,此前毕业于清华大学姚班。

论文标题:Emergence of Superposition: Unveiling the Training Dynamics of Chain of Continuous Thought
Paper:https://arxiv.org/abs/2509.23365v1
具体来说,他们通过对一个简化的两层 Transformer 在「图可达性问题」上的训练动态进行理论分析,将训练过程划分为两个阶段:
思维生成(thought generation)阶段:模型自回归地生成一条连续思维链;
预测(prediction)阶段:模型利用已生成的思维进行最终预测。
值得注意的是,通过对思维生成阶段进行分析,该团队揭示了一个重要现象:即便每个训练样本只包含一个演示样例,叠加(superposition)仍然会在训练中自发涌现。
他们的理论分析与实验结果均表明,当采用连续思维训练(Coconut 方法)时,索引匹配 logit(index-matching logit)(衡量模型局部搜索能力强度的一个关键指标)在温和假设下保持有界(bounded)。这与传统 Transformer 分析截然不同 —— 后者在无连续思维的情况下,logit 会呈对数增长并趋于无界。
一个有界的索引匹配 logit,能在「探索」与「利用」之间维持动态平衡:
若 logit 过小,模型无法有效进行局部搜索,下一步几乎只能随机猜测;
若 logit 过大,模型则会过度自信地锁定某一条局部路径(例如仅凭节点入度等局部特征),从而过早排除真正正确的路径。
而当 logit 保持在适度范围内时,模型既能利用局部结构,又能为多条合理路径分配相近的权重,这便自然形成了叠加式推理(superposition reasoning)。这也回答了之前论文未能解答的问题 —— 为何叠加态会在训练中自发涌现。
这里我们就不深入其理论证明部分了,感兴趣的读者请查看原论文。下面简单看看其实验部分。
实验与结果
为了验证其理论分析的结果,该团队使用了一个 GPT-2 式解码器进行实验,其包含两层 Transformer(d_model=768, n_heads=8)。
该模型是从零开始训练的,优化器为 AdamW(β₁=0.9,β₂=0.95,权重衰减 10⁻²),学习率固定为 1×10⁻⁴,全局 batch size 为 256。数据集则来自 ProsQA 的一个子集。
训练策略方面,按照之前的方法,他们采用多阶段训练,并使用思维链示范进行监督。
在阶段 c,模型学习在预测推理路径上第 c 个节点之前使用 c 个连续思维(即思维生成阶段)。
当 cl(思维链长度)时,模型在生成 l 个连续思维及A标记后,预测最终答案(即预测阶段)。
训练共 350 个 epoch:阶段 1 训练 150 个 epoch,后续每阶段 25 个 epoch。在每个阶段中,以 0.1 的概率混入之前阶段的数据,以防遗忘。最终模型在测试集上的准确度为 96.2%。
思维生成阶段
为分析 L^coco 下 μ_v 的训练动态,该团队追踪了第二层注意力的 logit 变化。当模型生成第 c 个连续思维时,μ_v 对应于源节点位于 N_c 的边 tokene的 logit。
在实践中,L^coco 会鼓励模型聚焦于当前搜索前沿,而非已探索的节点,因此注意力主要集中在「前沿边 (frontier edges)」上,即源节点位于 N_c \ N_{c−1} 的边。
为简化理论分析,该团队假设 μ₂=0,但在实际训练中,模型会对其他边也赋予非零注意力。因此该团队报告的是测试集上前沿边与非前沿边之间的 logit 差值,以更准确反映 μ_v 的有效变化。
结果见图 2。
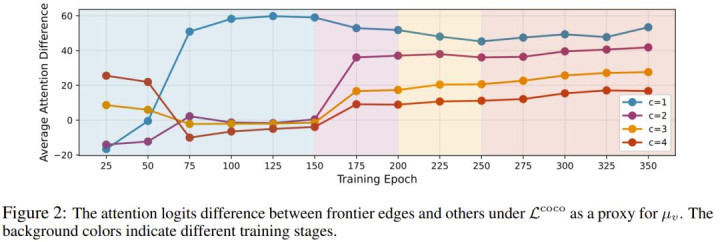
在阶段 1(蓝色背景)中,模型在预测第一个连续思维(c=1)时,逐步学会了关注前沿边。logit 差值稳步上升,并在约 125 个 epoch 后稳定于 60 附近,与定理 1 的理论预测一致:在 L^coco 下,μ_v 先增长后趋于稳定且有界。

当切换到阶段 2(紫色背景)时,模型在生成第二个连续思维(c=2)时所需的收敛 epoch 大幅减少。更有趣的是,这种模式可推广至 c=3 和 c=4,尽管模型从未显式训练生成超过两个思维。

这种「长度泛化(length generalization)」表明:一旦叠加态在早期阶段涌现,后续阶段便能快速复用它,进一步拓展搜索前沿。
该团队还使用了 L^BFS 的变体(COCONUT-BFS 方法)进行对比。与 L^coco 不同,在 c=1 时,注意力 logit 差值没有饱和,而是持续增长到更高水平,这与定理 1 的分析一致。
答案预测阶段
接下来该团队分析了模型如何预测最终答案。根据引理 2,预测依赖两个信号:
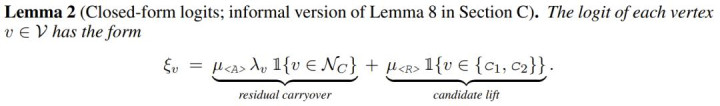
残差信号(residual carryover),它将最后一个思维 [t_C] 中已探索的节点以强度 μ_A 传递至答案 tokenA。具体来说,这对应于第一层从A到 [t_C] 的注意力,用于复制可达节点的叠加状态。
候选提升信号(candidate lift),它以强度 μ_R 提升两个候选节点的 logit。由于R在第一层中复制候选节点,因此第二层从A到R的注意力可视为 μ_R 的智能体。
图 3 展示了两者的训练动态。
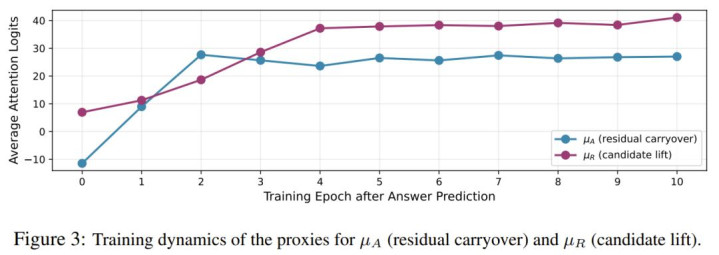
一旦进入预测阶段,μ_A 与 μ_R 都迅速上升,并在约 5 个 epoch 后趋于稳定。这与定理 3 的结论一致:μ_A 与 μ_R 以相似速率增长,确保正确候选 c⋆ 的 logit 最高。

与理论中的无界增长不同,该团队在实践中观察到 logit 实际上会趋于平台期。这可能是因为实际训练中,预测阶段仍与思维生成阶段相互作用,而理论假设思维分布固定,以便单独分析 μ_R 与 μ_A 的关系。该团队将这一差异留待了未来研究。
总结
本文研究了在连续思维链训练中叠加态的自发涌现机制。该团队对一个简化的两层 Transformer 在有向图可达性任务上的训练动态进行了系统的理论分析。
结果显示,在温和假设下,索引匹配 logit(衡量模型局部搜索能力的关键指标)在训练过程中会保持有界。
一个有界的 logit 能有效平衡「探索」与「利用」配资平台股票配资,从而让模型在推理中实现隐式的并行思考,自然产生叠加现象。
配资通提示:文章来自网络,不代表本站观点。